递归：程序执行过程中，调动自身的编程技巧称之为递归，如果你需要了解更多关于递归的说明，可以移步下面的链接查看百度百科。好吧，我们这里不谈递归的概念，只谈实现

在去实现递归之前，先来看一个小🌰例子：

def a():
    print('Polar Snow')

def b():
    return a()

def c():
    return b()

def d():
    return c()

d()

------------
Polar Snow

如代码所示，我执行了d()，但是在d的内部又执行了c(),在c的内部又执行了b(),在b的内部执行了a()，调用关系如下图所示：

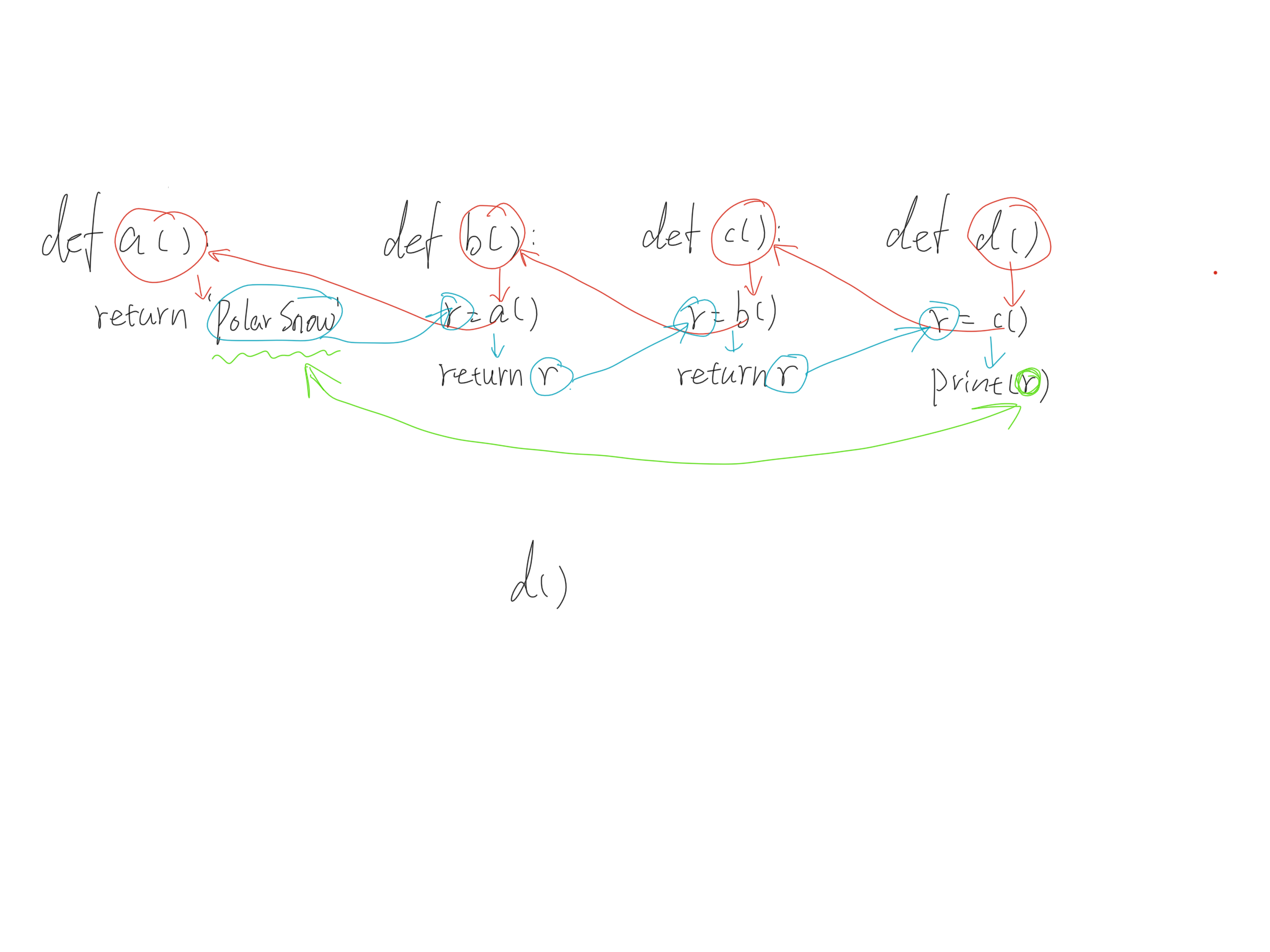
执行d()的时候，先走红色线的调用，到a()后，走蓝色线的返回值，最后的print(r)实际上就是a()函数的返回值

递归

了解了上面的例子后，会更容易递归的实现，现有如下递归实例：

def func(n):
    n += 1
    if n >= 4:
        return 'end'
    return func(n)

r = func(1)
print(r)

------
end

红色的线是调用线，蓝色的线是返回线。可以看到，递归是逐层调用，当条件满足时结束调用自己，并逐层将值返回。上面的案例中，每层的值都是按照原值进行返回，在实际应用中，可以对每下一层返回的值进行计算后再返回给上一层。

思考题

使用递归的方式计算：7的阶乘

def cal(n):
    if n == 0:
        return 1
    return n * cal(n-1)

print(cal(7))

------------
5040

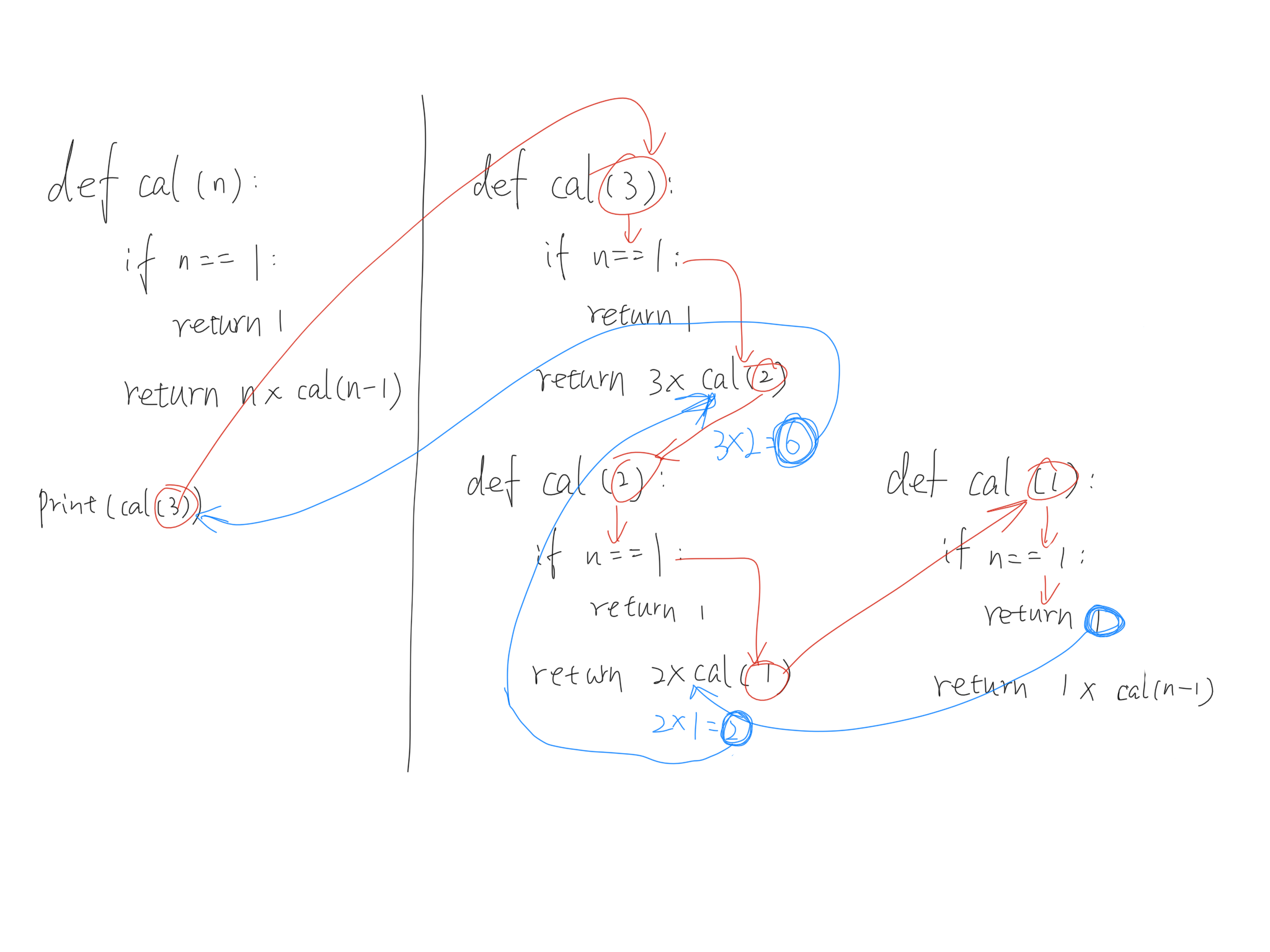
使用递归的方式计算：1*2*3*4*5*6*7

def cal(n):
    if n == 7:
        return n
    return n * cal(n+1)

print(cal(1))

------------
5040

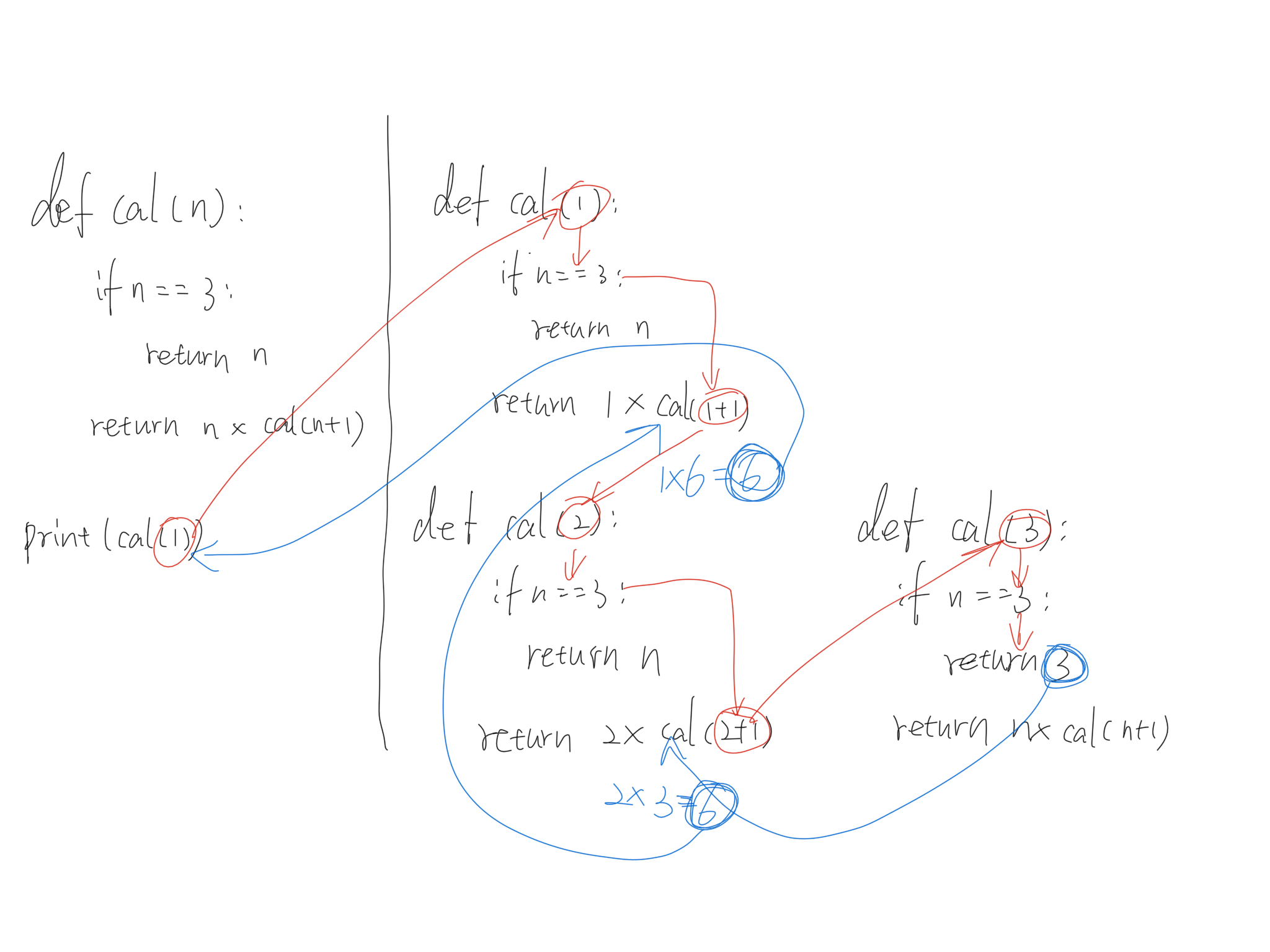
总结：从以上两种对递归的使用来看，可以总结出，递归计算的两个关键点

return点：递归到第几层的时候开始返回，返回什么？
计算点：当下一层的函数返回数据的时候，需要对数据做什么样的计算？

第一种计算阶乘的思路是传递一个最大值，让函数帮我从大往小乘。有了这个信息就确定了计算点的方式！是从大往小乘，大的值就是原参数的值，小的值是通过下一层计算得来的，所以就确定了计算点的表达式n * cal(n-1)。最后还需要确定递归的第一个返回值，也就是return点，既然是从大往小乘，return点就是最小值1，阶乘算到1就不用往下算了，所以在递归中加入判断，当值=1时，返回1.

第二种计算阶乘的思路是传递一个最小值，在递归内部，写死了计算到7的阶乘，递归到最深层的时候返回7到上一层，交给上一层的n * 7表达式来处理，由于函数中，每层的调用n都加了1，那么此时的n肯定是6，所以表达式会计算6 * 7,并将结果42返回给上一层。而再上一层的n肯定是5，所以又会去计算5 * 42并将结果返回至上层

Polar Snow Documentation

Python for 递归

递归